
目前一些移动端的皮肤材质采用的是2011年Eric分享的Pre-integrated Skin Shading的精简版,主要是利用$N\cdot L$与模型表面的曲率去采样预计算的LUT图,并将结果作为新的NoL来计算漫反射的颜色。但现在很多3D手游的带宽比较吃紧,而ALU占用率不是很高,而且不少手机GPU芯片还在不断增加ALU,那么将采样LUT图的方式转换为纯算术的方式岂不美哉。
骑手日记
五一送外卖的间隙翻到了一篇博文,原文作者Matt是Ready At Down工作室(开发了《教团:1886》)的图形工程师,他简述了一种使用Spherical Gaussian(球面高斯函数,以下简称SG)近似预积分SSS材质的方式。虽然Matt只是抛出一个不完整的思路供大家参考和讨论,但我实际操作后觉得效果还不错。
下面开始踩坑,错误的地方请各位老板不要给差评,一个差评白跑一天。
Spherical Gaussian
参考资料
SG是比较冷门的话题,但Ready At Dawn工作室却对其情有独钟,并使用在自研的游戏引擎中,其效果也经《教团:1886》得到验证:
2016年Matt在个人博客中编写了6篇关于光照贴图烘焙与SG实际应用的博文。其中很多算法和实现思路都是参考龚大(叛逆者)的论文。我也将重要的前5篇翻译到了自己的博客,感兴趣的老铁可以戳戳。
什么是SG?
高斯函数和用于图像处理的二维高斯函数比较常见的,而SG就是三维空间中分布在球面上的高斯函数。
一维的高斯函数的形式是:
\begin{align}
ae^{\frac{-(x-b)^{2}}{2c^{2}}} \nonumber
\end{align}
(x-b)项使一维高斯函数在笛卡尔坐标系中可以求出给定点到高斯中心的距离。而三维的球面高斯函数参数与一维和二维的不同,需要改变(x-b)项,让高斯函数根据两个标准化的方向向量夹角进行计算使其作用在球面上。用点积的方式就可以实现:
\begin{align}
G(v;\mu,\lambda,a) = ae^{\lambda(\mu\cdot{v}-1)}\nonumber
\end{align}
和普通高斯函数一样,有一些参数可以控制波瓣的形状和位置。参数\mu是波瓣的轴向或方向,控制波瓣在球面的位置并且指向波瓣的中心;参数\lambda是波瓣的sharpness(锐度),增加该值时,波瓣会变得更纤细,也就意味着越是远离波瓣轴衰减的越快;参数a是波瓣的振幅或者强度,是波瓣波峰顶部的高度值,可以是标量值,在图形学中也可以是向量,来控制RGB不同颜色通道的变化。在HLSL代码中,只需要球面上一点的标准化方向向量就可以求出该点的球面高斯值。1
2
3
4
5
6
7
8
9
10
11
12struct SG
{
float3 Amplitude; // float3或者float皆可,按需求设定
float3 Axis;
float Sharpness;
}
float3 EvaluateSG(in SG sg, in float3 dir)
{
float cosAngle = dot(dir, sg.Axis);
return sg.Amplitude * exp(sg.Sharpness * (cosAngle - 1.0f));
}
为何使用SG?
SG非常直观易于理解,而且很多论文已经探索了SG的使用价值,并使用SG对材质的漫反射和镜面反射实现了预计算的辐射率传递(pre-computed radiance transfer, PRT)。尤其是龚大的《All-Frequency Rendering of Dynamic, Spatially-Varing Reflectance》一文成为RAD工作室使用球面高斯函数的主要参考和灵感。SG有以下几个特点:
两个SG做积运算可以得到另外一个SG;
\begin{align}
G_1(v)G_2(v) = G(v;\frac{\mu_m}{||\mu_m||},a_1a_2e^{\lambda_m(||\mu_m||-1)}) \nonumber
\end{align}计算整个球面的SG积分可以得到SG的总“能量”,对光照计算很有用;
\begin{align}
\int_{\Omega}G(v)dv = 2\pi\frac{a}{\lambda}(1-e^{-2\lambda}) \nonumber
\end{align}两个SG也可以做点积运算,求出两个SG乘积的积分。
\begin{align}
\int_{\Omega}G_1(v)G_2(v)dv = 2\pi{a_0}{a_1}\frac{e^{||\mu_m||-\lambda_m}-e^{-||\mu_m||-\lambda_m}}{||\mu_m||} \nonumber
\end{align}
使用SG近似漫反射光照和镜面光照的详细内容可以看Matt的原文或者戳我的博客。
与SSS何干?
Matt给出了下方的代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16float3 diffuse = nDotL;
if(EnableSSS)
{
// Represent the diffusion profiles as spherical gaussians
SG redKernel = MakeNormalizedSG(lightDir, 1.0f / max(ScatterAmt.x, 0.0001f));
SG greenKernel = MakeNormalizedSG(lightDir, 1.0f / max(ScatterAmt.y, 0.0001f));
SG blueKernel = MakeNormalizedSG(lightDir, 1.0f / max(ScatterAmt.z, 0.0001f));
// Compute the irradiance that would result from convolving a punctual light source
// with the SG filtering kernels
diffuse = float3(SGIrradianceFitted(redKernel, normal).x,
SGIrradianceFitted(greenKernel, normal).x,
SGIrradianceFitted(blueKernel, normal).x);
}
float3 lightingResponse = diffuse * LightIntensity * DiffuseAlbedo * InvPi;
思路是根据光源朝向和红、绿、蓝三种不同的散射强度创建三个SG核,这三个SG滤波核其实就是模拟红绿蓝三种波长的Diffusion Profile。结合2011年Eric的预积分皮肤PPT来看,根据剖面图可以看出红光比绿光和蓝光散射的更远,因此会出现白色——黄色——橙色——红色——黑色的渐变效果。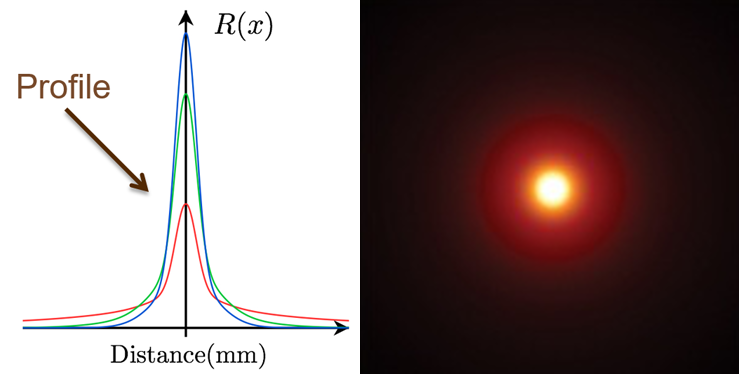
因此可以用一个float3 ScatterAmt表示散射强度, x分量表示红光,依此类推。而构建SG时,\lambda参数表示锐度,\lambda数值越大表示越细长。因此红光的\lambda值最小,那么可以简单的用$\frac{1}{ScatterAmt.x}$来表示红光,依此类推。
按照Matt原文的描述,首先是归一化的SG核,然后代表轴向的$\mu$与光源对齐,代表振幅的与
光源强度(也可认为是LightColor)相乘。可以推出下面的代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14// SG Kernel
FSphericalGaussian MakeNormalizedSG(float3 LightDir, half Sharpness, half3 LightIntensity)
{
// 归一化的SG
SphericalGaussian SG;
SG.Axis = float3(0, 1, 0); // 任意方向
SG.Sharpness = Sharpness; // (1 / ScatterAmt.element)
SG.Amplitude = SG.Sharpness / ((2 * PI) - (2 * PI) * exp(-2 * SG.Sharpness)); // 归一化处理
// 对齐轴向,乘上光源强度(颜色)
SG.Axis = LightDir;
SG.Amplitude *= LightIntensity;
return SG;
}
因此虽然此函数的名字叫MakeNormalizedSG,但其整个球面积分值已经是乘过光源强度的了,不一定是1。当时我认为Matt可能这里有错误,但我还是too yound, too cai了。因为他后面使用了函数SGIrradianceFitted()来近似渲染方程中的$L_i$与cosine项点积的积分,但这个函数是Stephen Hill提出并且针对归一化SG的,Amplitude项并不会参与计算。所以Matt才在最后一行把光源强度加入计算。破案了,MMP坑了我有一会儿,让我有种文章描述前后矛盾的错觉。SGIrradianceFitted()函数在SG系列的第三篇有写到。是一种比较精确的逼近光源SG与余弦波点积做积分的方式。另外两种较粗糙的近似方式可以看那篇文章。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29float3 SGIrradianceFitted(in SG lightingLobe, in float3 normal)
{
const float muDotN = dot(lightingLobe.Axis, normal);
const float lambda = lightingLobe.Sharpness;
const float c0 = 0.36f;
const float c1 = 1.0f / (4.0f * c0);
float eml = exp(-lambda);
float em2l = eml * eml;
float rl = rcp(lambda);
float scale = 1.0f + 2.0f * em2l - rl;
float bias = (eml - em2l) * rl - em2l;
float x = sqrt(1.0f - scale);
float x0 = c0 * muDotN;
float x1 = c1 * x;
float n = x0 + x1;
float y = saturate(muDotN);
if(abs(x0) <= x1)
y = n * n / x;
float result = scale * y + bias;
return result;
}
好的gays,理论暂时告一段落,整活。
UE4中实现移动端的SGSSS
添加着色模型
为延迟渲染添加着色模型的流程我照着外网学习了一波并记录在博客中。这次是针对移动端添加新的着色模型,相比为延迟渲染管线需要修改的地方比较少。首先打开你辛辛苦苦下载的UE4.24源码,在EngineTypes.h中为EMaterialShadingModel添加枚举成员,DisplayName材质编辑器UI中的名称。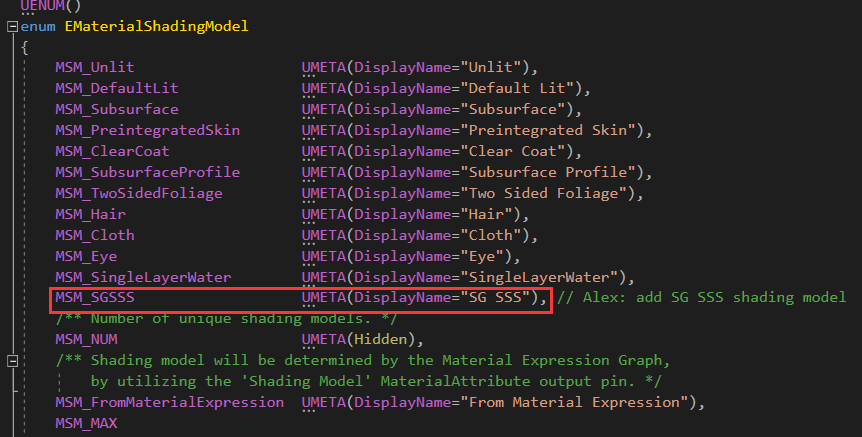
然后在MaterialShader.cpp中添加着色模型的名称,该名称是在源码内使用的(非UI):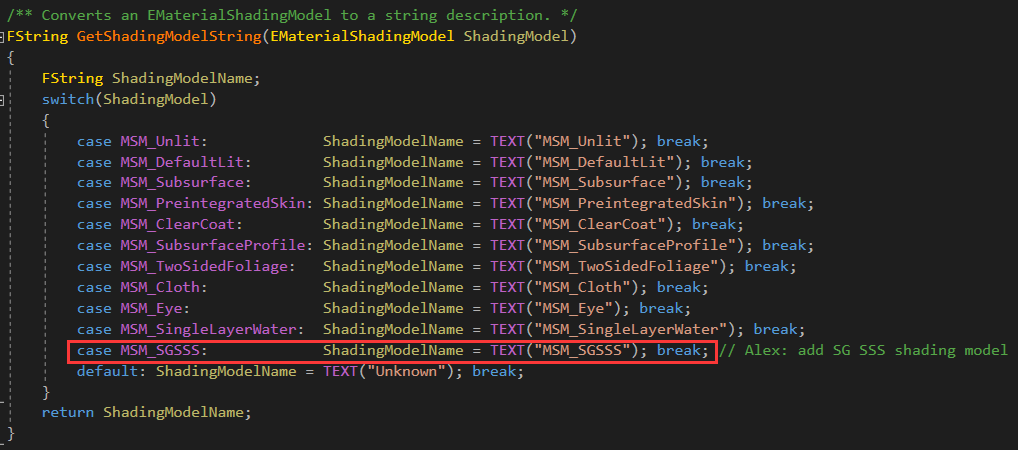
然后修改HLSLMaterialTranslator.h,编译着色器时为SGSSS添加类型描述宏:
我们将会需要两个材质引脚——Scatter Amount(三维向量)和Curvature(标量,后面会用到)。为了不影响其他引脚的正常使用,我们选择Subsurface和Custom0引脚作为这两个参数的输入接口。在Material.cpp中做修改: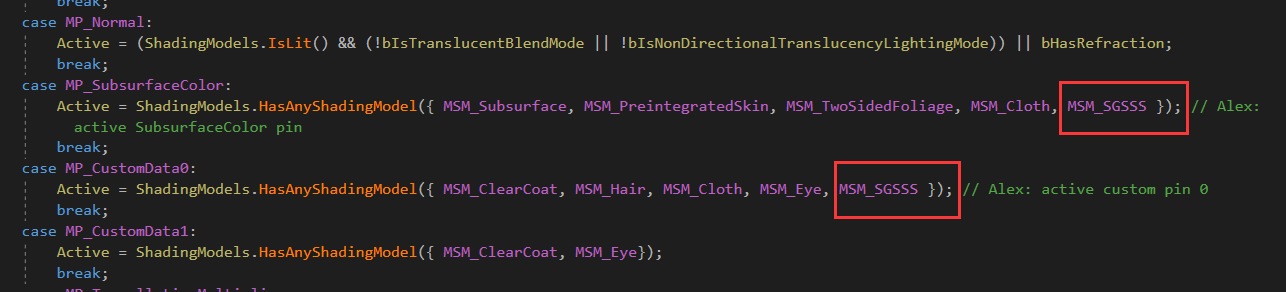
然后在MaterialGraph.cpp中修改引脚的名字,更加直观清晰: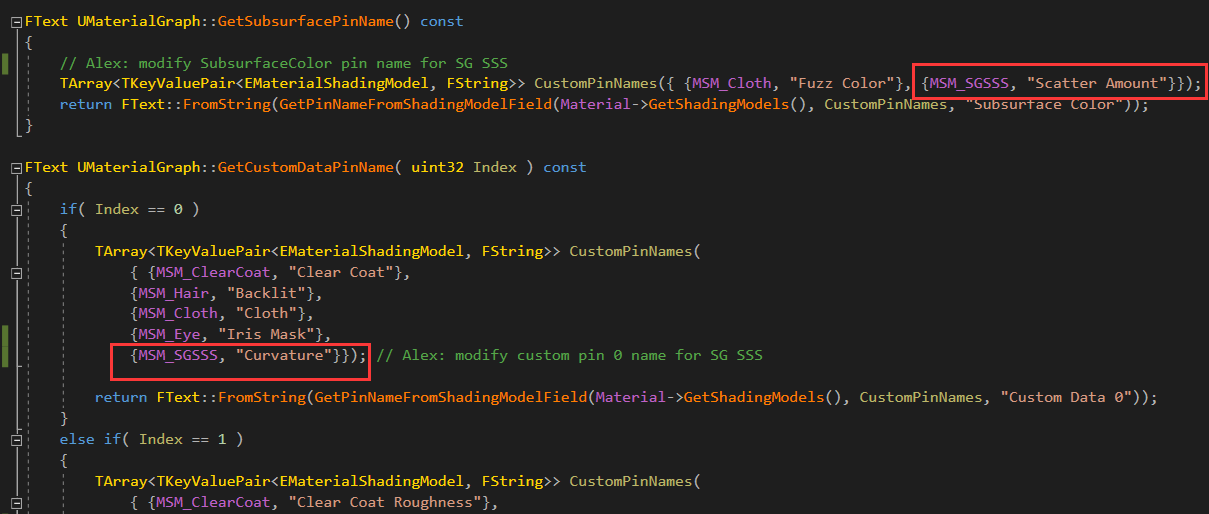
一切搞定, 了吗?并没有。UE4在编译着色器时会检查冗余和不支持的内容然后丢弃掉或者使用默认值替代。在HLSLMaterialTranslator.h中有这么一段代码: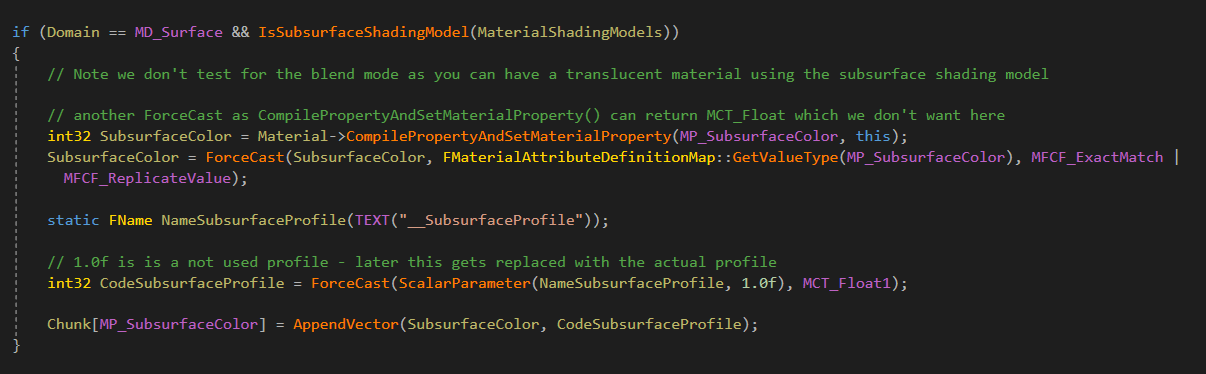
会通过IsSubsurfaceShadingModel()函数来检查你选择的着色模型是否属于Subsurface类,不是的话就不会编译该引脚的输入,那不是白搞事了?所以打开MaterialShared.h,为Subsurface类添加SGSSS:
这是耽误我送外卖的坑点之一。老板们,C++源码部分修改已经完事儿,编译走起来。
编写着色器
与延迟渲染管线比,移动端几乎不用修改.ush和.usf就可以取到值,当然这和GBuffer存储数据和提取数据有关。在开始编写代码前,建议开启着色器开发模型,可以自动报错方便调试。位置\Engine\Config\ConsoleVariables.ini。
首先添加一些与SG有关的函数,然而巧的是UE4已经使用龚大的SG算法来计算Bent Normal了,所以有些函数直接用就可以了。在SphericalGaussian.ush文件中,struct FSpherical Gaussian{}是SG的结构体,其中的Axis, Sharpness和Amplitude分别对应的是$ \mu, \lambda和a$;DotCosineLobe()其实就是Stephen Hill提出的SGIrradianceFitted()。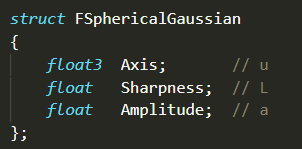
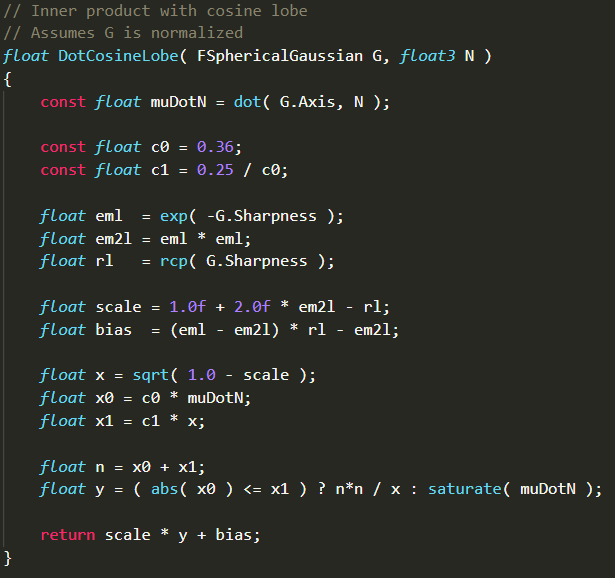
下面添加一个MakeNormalizedSG()函数创建归一化的SG,并且轴向为光源方向,锐度是$\frac{1}{ScatterAmt.element}$:
然后添加计算光照项与Cosine项的函数SGDiffuseLighting()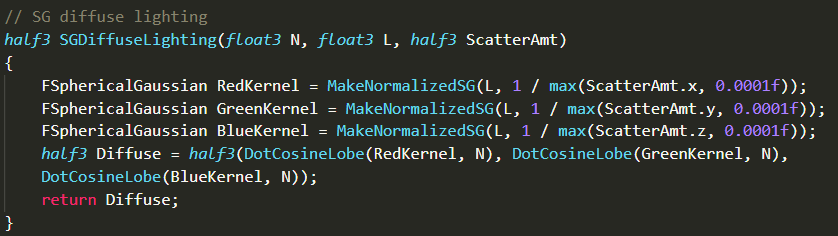
为了方便测试效果,下面先针对平行光的交互添加代码。在MobileBasePassPixelShader.usf添加头文件:
然后在平行光的渲染部分修改代码,可以看到实现方式类似预积分皮肤的方式,将SG结果作为新的NoL参与计算。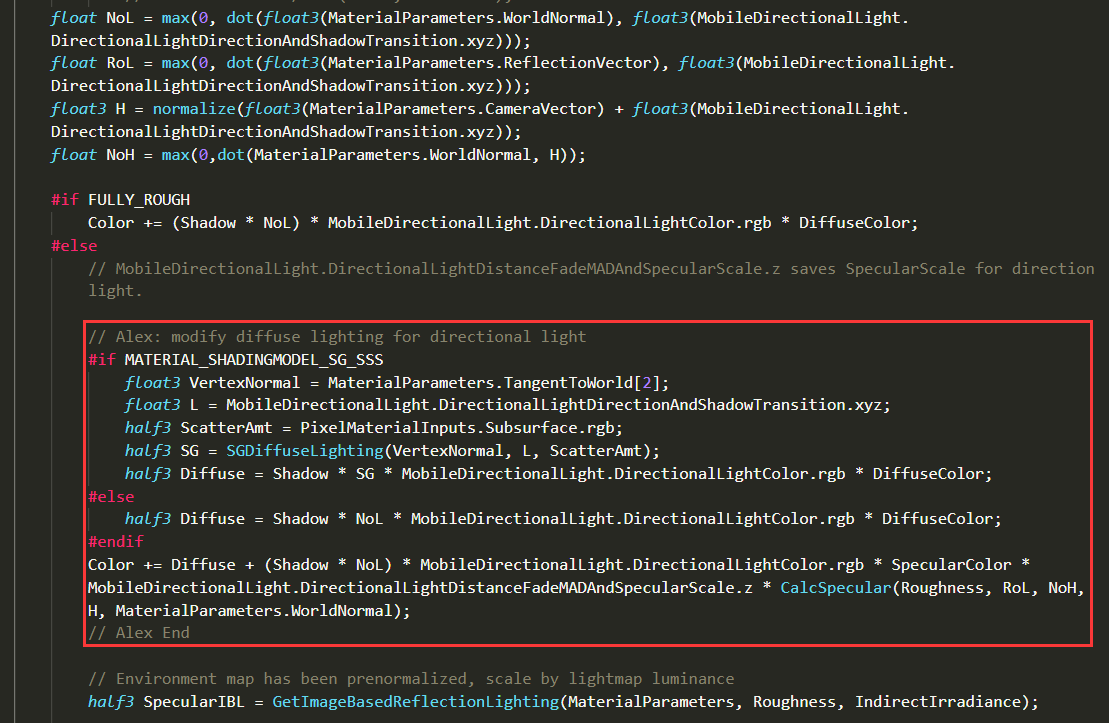
保存.usf文件后,万万不可在UE4工程中按ctrl + shift + .编译所有材质,那成千上万个需要编译的着色器分分钟让你被黑人抬棺。有很多控制台命令可以指定编译路径、文件或材质。我最常用的是recompileshaders material “Material Name”,比如我们创建个材质M_SGSSS,那么后面调试代码的时候每次只需要控制台输入recompileshaders material M_SGSSS即可,只编译此材质就会让黑人抬棺失败。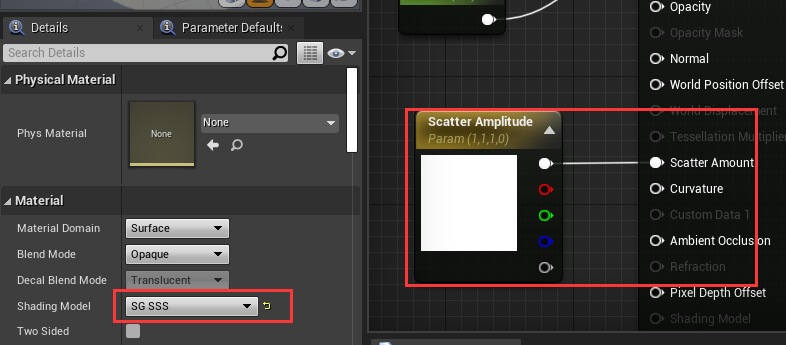
创建好材质之后,可以调节参数看效果。是不是有预积分内味儿了?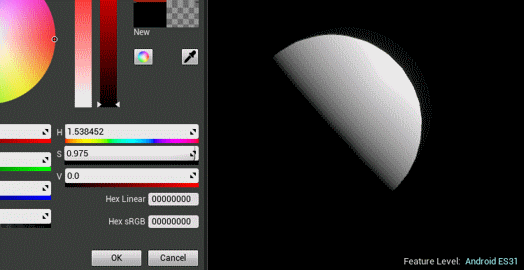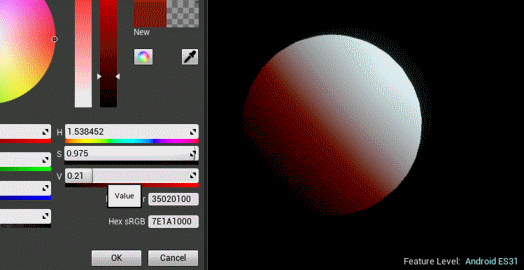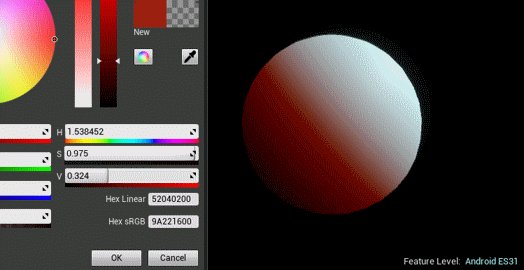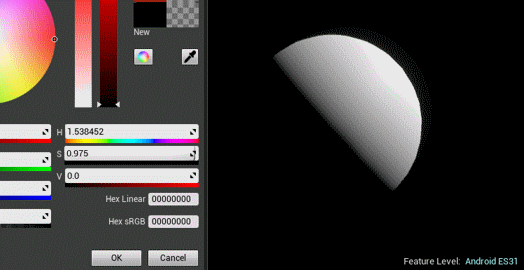
这个算法目前的瑕疵Eric也提到过,不使用filmic tone mapper的话会看到三色光扩散的范围很明显,用在皮肤上会看到蓝色分离的较明显,我们加上tone mapper对比一下,对比非常明显,经过tone mapping后的非常接近预积分色彩范围(暂时不考虑曲率)。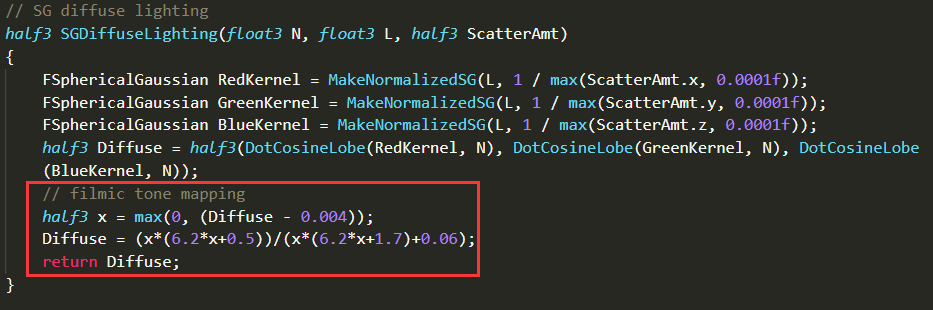

因为SG制作Diffusion Profile的自由度很高,可以制作各种SSS效果。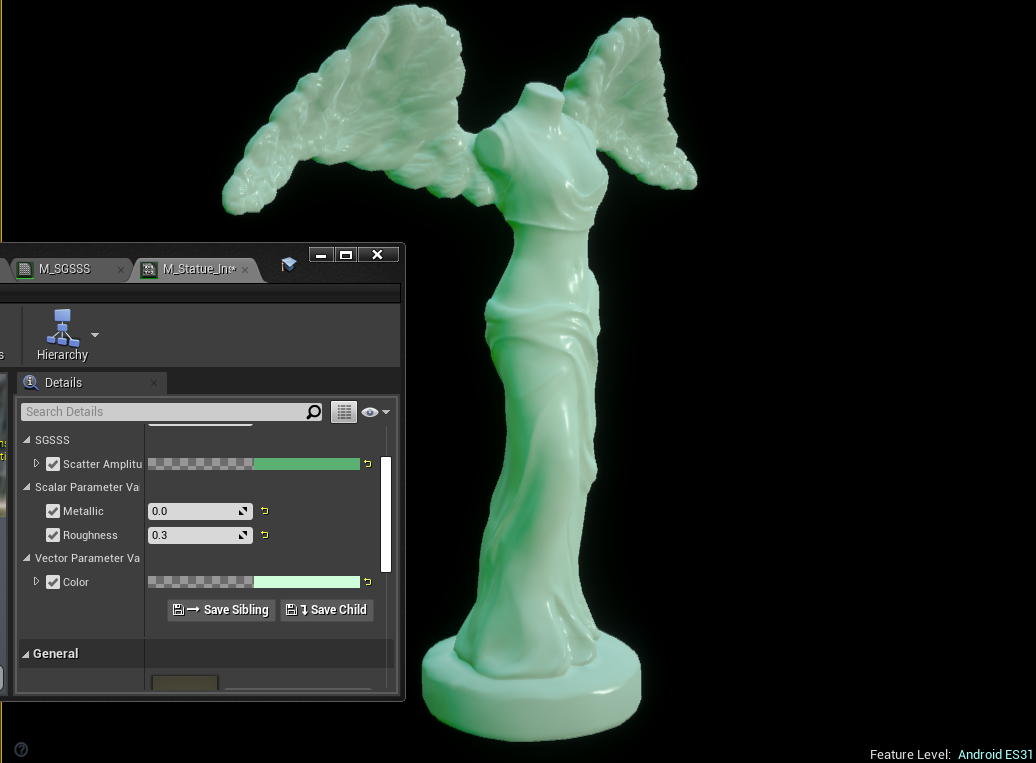
如果把同样的算法在点光源和聚光灯的部分实现,然后把一个点光源放到模型里面,效果也很不错。
加入曲率
预积分LUT的U方向采样利用的是NoL,我们已经实现了类似的效果。V向采样利用的是曲率。如果不追求较真实合理的效果,不做这一步也是可以的,会得到下面的效果。曲率高的鼻子和眼睛与曲率低的头顶的扩散剖面没区别。
那么按照Eric的方法求出曲率$\frac{1}{r}$: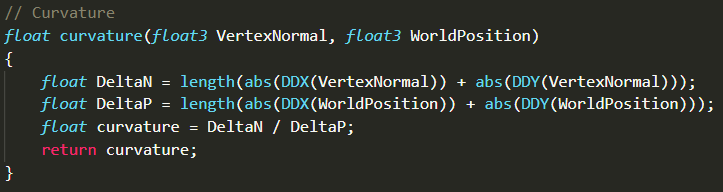

如果敢用这种计算出来的曲率绝对被主美打死。
那还是制作一张柔和过度的曲率图吧。如果使用Substance烘焙曲率贴图会发现可调的参数非常少,而且凹面的曲率是0,在鼻翼两侧、下巴、眼窝以及耳朵内部都会变成黑色,结果不正确(也可能我的substance是渣渣)。
于是使用Houdini,好处就是可以先将低面数模型细分一下,然后计算曲率。注意不要用官方提供的Labs中的烘焙贴图工具,那个问题很多且结果不准确。计算后的结果是作为顶点的Cd属性,可以给一个principle shader以顶点色作为base color,最后用bake texture输出出来。对比一下实时计算的效果完胜,缺点是占用带宽,且每个模型都要制作一张图。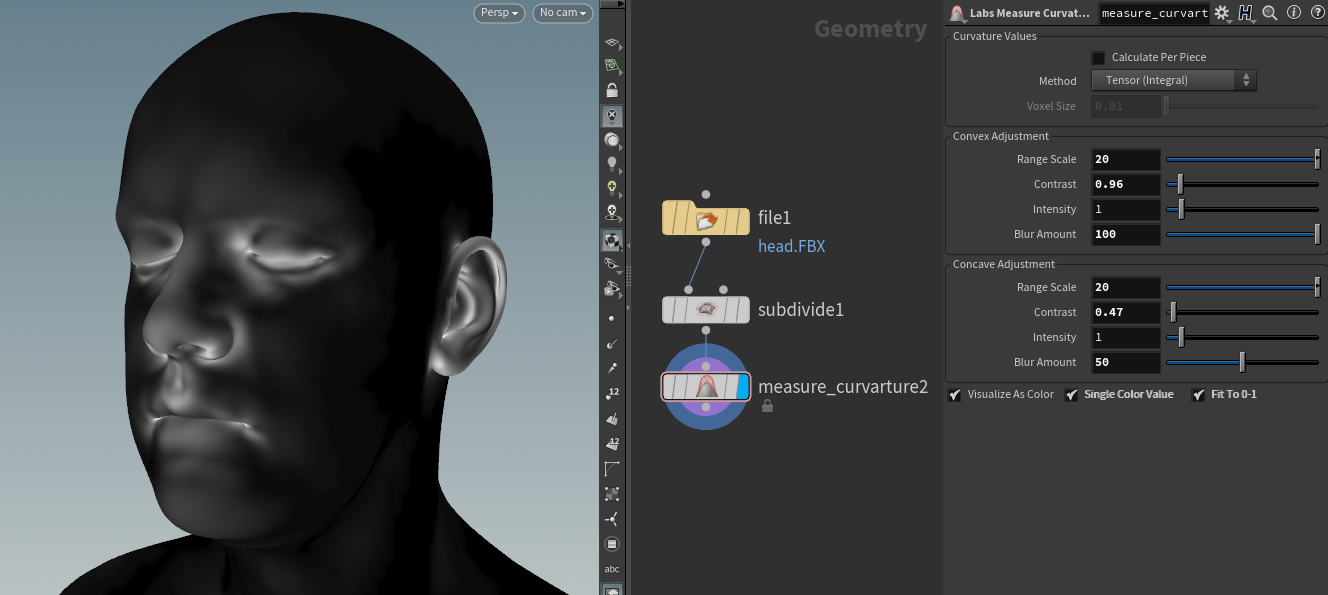

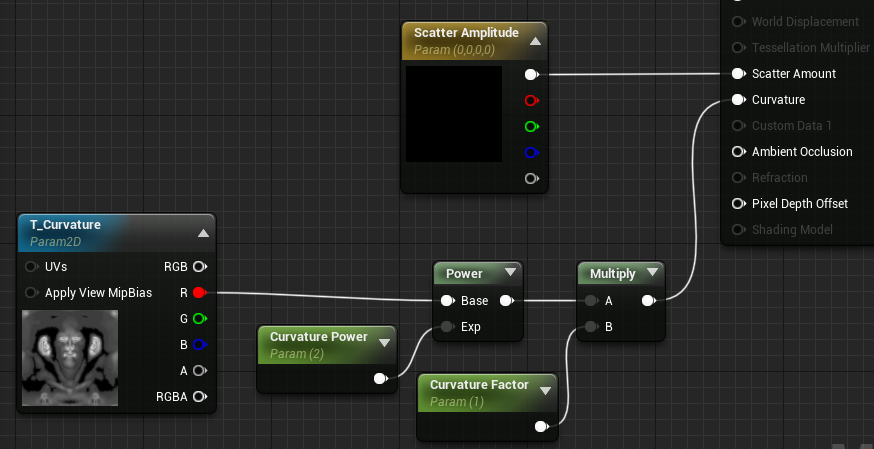
曲率越大扩散越强,那么可以尝试将Curvature与ScatterAmt相乘得到新的ScattrerAmt。并且可以在材质中对曲率贴图进行简单的对比度或强度等等方面的操作,这样更加灵活和自由。并且反复调试后我觉得还是不加tone mapper柔和含蓄一点。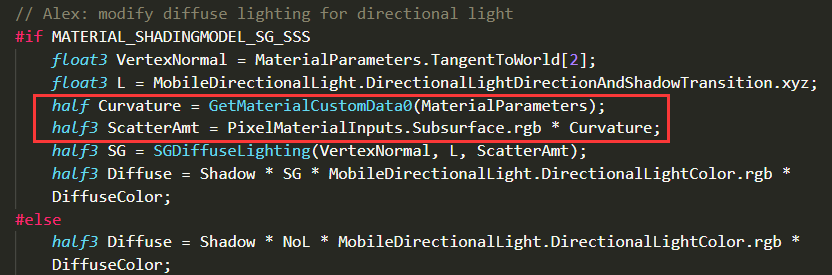




又有客户催单了,各位老板慢用,告辞。

