本篇是球面高斯函数与预计算光照系列的第三部分,上篇文章提到了球面高斯函数的一些属性,本文会讨论如何在渲染场景中使用这些属性并发挥它们的优势。
本系列的其他文章可以点击下方链接跳转。
天降高斯
假设表面的一个点x被光源L照亮,该光源由名为$G_L$的球面高斯函数表示。那么使用兰伯特漫反射BRDF计算出射光辐射率就是下方的公式:
对于精确光源来讲,本质上就是按比例缩放的三角函数,计算起来像$N\cdot{L}$一样简单。但如果使用区域光就会遇到麻烦,因为该积分没有闭式解。假设有一个奇特的高斯光源,它的角衰减可以由球面高斯函数精确地表示。如果在渲染公式中将高斯光源作为$L_i$,那么就是一个球面高斯函数与被限制范围(0-1)的余弦波做点积。上篇文章中提到过两个球面高斯做积运算的过程,那么不妨尝试将余弦波拟合成一个球面高斯函数,这样渲染公式中就是将两个球面高斯函数乘积的结果做积分了。根据Jiaping Wang等人的论文《All-Frequency Rendering of Dynamic, Spatially-Varing Reflectance》中的方法,将余弦波拟合到单个球面高斯函数时,$\lambda$=2.133,a=1.17。代码中的实现就会变成:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23SG CosineLobeSG(in float3 direction)
{
SG cosineLobe;
cosineLobe.Axis = direction;
cosineLobe.Sharpness = 2.133f;
cosineLobe.Amplitude = 1.17f;
return cosineLobe;
}
float3 SGIrradianceInnerProduct(in SG lightingLobe,
in float3 normal)
{
SG cosineLobe = CosineLobeSG(normal);
return max(SGInnerProduct(lightingLobe, cosineLobe), 0.0f);
}
float3 SGDiffuseInnerProduct(in SG lightingLobe, in float3 normal,
in float3 albedo)
{
float3 brdf = albedo / Pi;
return SGIrradianceInnerProduct(lightingLobe, normal) * brdf;
}
误差分析
毕竟是余弦波的近似值,肯定会有误差。最好的办法就是对比两者的曲线:
仅从图表上看,球面高斯显然与余弦波不太匹配。首先,波峰值超过了1,但必须确保曲线下方的面积与余弦波瓣尽量保持一致否则会导致能量损失。另外,球面高斯在球面上的任何地方的值都没有达到0,所以有很长的拖尾。这就意味着当逼近余弦波的球面高斯与精确光源进行积分时,光照会包裹整个球体,超过了N·L等于0的点。不过这种情况与球谐函数有类似之处,球谐函数也超过了$\frac{\pi}{2}$的位置,如下图所示:
使用球谐函数的情况下,近似值其实已经是负值了,或许比球面高斯的长拖尾更糟糕。L1球谐函数的近似值很差,L2球谐的近似值效果尚可。下图从左至右:振幅0-1的余弦波,逼近余弦波的球面高斯函数,L2球谐函数。
下面再看一下与球面高斯光源做计算得到漫反射光照的结果。蓝线代表双球面高斯做点积(球面高斯光源与逼近余弦波的球面高斯)。与之对比的是brute-froce数值积分求出的球面高斯与(振幅0-1)的余弦波的乘积。如图所示(球面高斯光源锐度=4.0):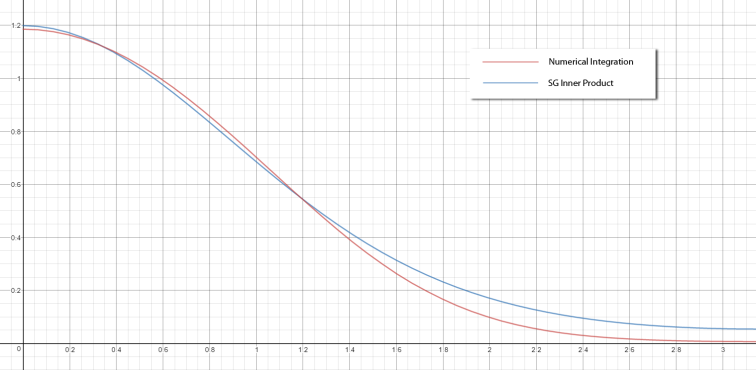
误差来自于对(振幅0-1)余弦波的近似球面高斯,而不是两个球面高斯点积的过程。最终辐射度的区别不是特别大,明显的区别就是背光区域,由双球面高斯点积的长拖尾导致的。下图使用锐度4.0的球面高斯光源,左为蒙特卡洛重要性采样计算的辐射度,右为与逼近余弦的球面高斯点积所得到的辐射度。
开销更低的近似方式
上篇文章提到过球面高斯的另外一个优点——波瓣绕轴对称,并且也讨论过如何计算球面的球面高斯积分从而获得总能量。那么可以尝试从积分中提出一些项,仅对球面高斯的轴朝向做计算。这必然会引入一些误差,但如果提出的项比较平滑,那误差还是可以接受的。公式的变化如下:
HLSL代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13float3 SGIrradiancePunctual(in SG lightingLobe, in float3 normal)
{
float cosineTerm = saturate(dot(lightingLobe.Axis, normal));
return cosineTerm * 2.0f * Pi * (lightingLobe.Amplitude) /
lightingLobe.Sharpness;
}
float3 SGDiffusePunctual(in SG lightingLobe, in float3 normal,
in float3 albedo)
{
float3 brdf = albedo / Pi;
return SGIrradiancePunctual(lightingLobe, normal) * brdf;
}
如果将这种近似方式以曲线形式和之前的作比较,会看出较大的差别。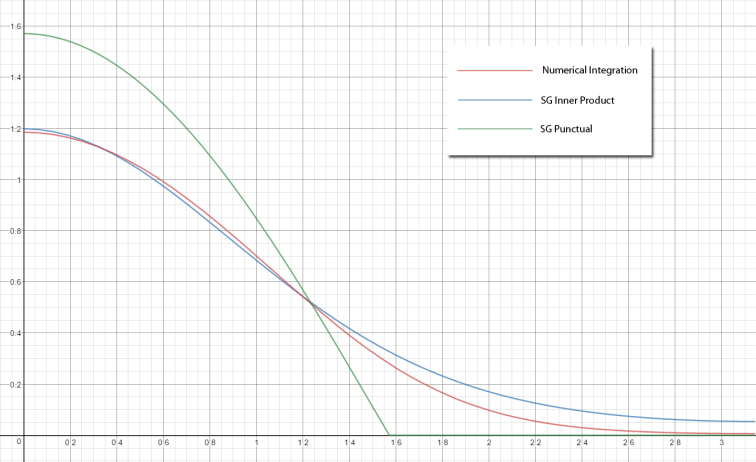
可以发现绿线代表的是开销较低的近似方式,而曲线的走势是限制范围的余弦波的缩放版本。但是这种近似方式开销非常低,已经将球面高斯函数转成了点光源。
更精确的近似
Stephen Hill提出了一种与球面高斯和余弦波积分匹配度非常高的近似方式。他的实现是针对归一化的球面高斯的,但是我们可以计算积分并缩放得到我们需要的结果。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29float3 SGIrradianceFitted(in SG lightingLobe, in float3 normal)
{
const float muDotN = dot(lightingLobe.Axis, normal);
const float lambda = lightingLobe.Sharpness;
const float c0 = 0.36f;
const float c1 = 1.0f / (4.0f * c0);
float eml = exp(-lambda);
float em2l = eml * eml;
float rl = rcp(lambda);
float scale = 1.0f + 2.0f * em2l - rl;
float bias = (eml - em2l) * rl - em2l;
float x = sqrt(1.0f - scale);
float x0 = c0 * muDotN;
float x1 = c1 * x;
float n = x0 + x1;
float y = saturate(muDotN);
if(abs(x0) <= x1)
y = n * n / x;
float result = scale * y + bias;
return result * ApproximateSGIntegral(lightingLobe);
}
其结果非常接近实际情况,并且可能开销比两个球面高斯点积更低。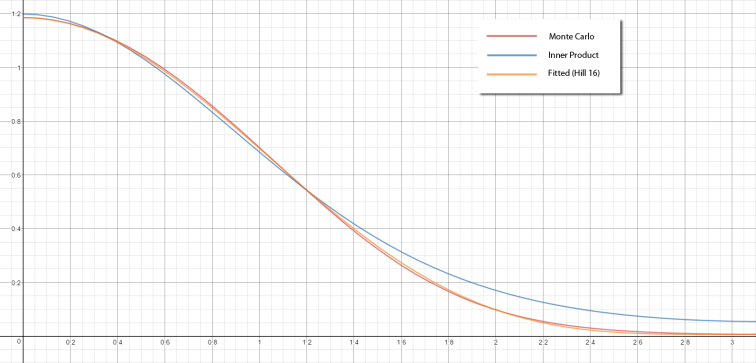
在球体上对比结果——左侧是两个球面高斯点积,中间是蒙特卡洛重要性采样所得结果,右侧是Stephen Hill的近似方式。

