球面高斯函数(Spherical Gaussian, SG)是比较冷门的话题,但Ready At Dawn工作室却对其情有独钟,并使用在自研的游戏引擎中。其效果也经《教团:1886》得到验证。本系列是由Ready At Dawn工作室的首席图形和引擎工程师Matt Pettineo编写在自己的博客。我将该系列的学习笔记记录于此,与大家分享。
原作者把球面高斯函数及其应用分为6篇介绍:
开始前,可以看一下文中用到的术语符号:
早期的方式
自从有了彩色的3D游戏,就有了预先计算光照贴图的方法,一直延续到现在(2020年)。原理比较简单:为每个纹素预先计算光照数值,然后在游戏运行时对光照数值进行采样来计算表面的最终效果。虽然原理简单,但细节就比较讲究了。比如将“光照”存储在纹理中到底意味着什么?或者计算的到底是什么值?在最早期,从光照贴图中获取的数值只是简单的与材质的漫反射颜色相乘,然后直接输出颜色到屏幕上。一般我们用以下的渲染公式计算从一个入射点计算出射辐射率:
暂且不考虑伽马矫正和sRGB转换等等,根据上面的描述,如果用普通的漫反射BRDF项(即$\frac{C_{diffuse}}{\pi}$)代替BRDF项,那么就会变成:
可以看到将右侧的常量项$\frac{C_{diffuse}}{\pi}$提到积分外,这样右侧复杂的积分运算就是预计算(pre-computed)的纹素了,因为光照贴图每个纹素存储的都是单一的固定颜色值,所以可以不用考虑观察方向,在运行时用常量项与每个纹素值相乘就是最终的颜色了。右侧的积分计算的是入射光辐射度,因此光照贴图中存储的就是入射光辐射度。实际上大多数的游戏并没有在运行时应用$\frac{1}{\pi}$,因为这是个常数项,为了降低开销可以也将这个常数项预计算在光照贴图中,这样只剩$C_{diffuse}$是在运行时参与计算的。这种情形下,实际存储的就是反射率。换言之,可以认为存储的值是当$C_{diffuse}=1.0$时漫反射的反射率,即具有漫反射BRDF的表面最大出射光辐射率。
法线贴图
光照贴图的核心概念之一就是利用空间域中以不同密度存储的数据来重建表面的最终效果。简言之,使用一个纹素密度存储光照贴图,并与不同密度(一般更高)的反射率贴图(albedo map)结合。这样无需计算每个纹素的辐射度积分就可以保留高频细节。但如何让辐射度根据其他纹理贴图(不仅仅是反射率贴图)变化呢?为了满足这种需求,在2000年初法线贴图开始被广泛使用,但仅限于与精确光源(punctual light source)计算时使用。并且法线贴图对光照贴图不起作用,因为光照贴图只存储了辐射度的比例值(标量),那么相比于直接光照区域,仅有环境光照(ambient lighting)的区域就非常的平整。如下图:
为了让光照贴图与法线贴图正确计算,光照贴图每个纹素不再存储单个标量值,而是辐射度的分布信息。法线贴图包含一定范围的方向分布信息,这些方向一般限制在表面上一个点的法线周围半球内。所以光照贴图存储的辐射度分布信息也是定义在同一个半球内的。V社(Valve)使用自研的Source引擎在《半条命2》中最早使用了这种分布,被称为“辐射度法线贴图”(Radiosity Normal Mapping)。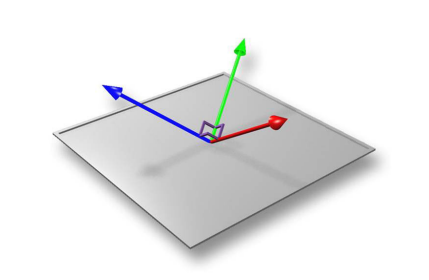
V社修改了光照贴图烘焙器算法,计算三个值而不是一个值,通过投影辐射度到上图中某一个基向量(basis vector)上得到三个值。游戏运行时,会基于法线贴图中的方向与三个基向量的夹角余弦值来混合光照贴图中的三个值从而得到辐射度值(通过开销很低的点积就可以计算)。这样就可以根据法线贴图中的方向有效地改变辐射度,进而避免了仅有环境光的区域过于平整的问题。
这个方式解决了静态物体的问题,对动态的物体和角色应用预计算的光照依然有问题。一些早期游戏(如《Quake》)用了一些技巧,例如在角色脚部位置采样光照贴图的数值,并使用该数值计算出环境光数值应用到整个模型上。而有些游戏的处理方式更粗糙,只把动态灯光和一个全局的环境光项结合使用。V社使用了更复杂的方法,将半球光照贴图基础扩展成由6个正交基向量形成的球面基础。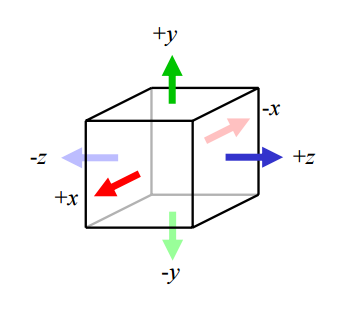
基向量与一个单位立方体的六个面朝向重合,V社称之为“环境立方体”。使用他们的基函数(basis functions)将辐射度投影到空间中一点周围的所有方向上(而不是面法线周围的半球上),动态的模型可以对任意法线方向采样辐射度来计算漫反射光照。这种形式被称为“光照探针”(lighting probe)或简称“探针”(probe)。
镜面反射
通过V社提出的方法,可以使用高频的法线贴图与光照贴图进行计算得到漫反射光照。为了让画面更真实,还需要支持更加复杂的BRDF,包括受观察方向影响的镜面反射BRDF。《半条命2》通过预生成(pre-generating)的立方体贴图和手动摆放的探针来处理环境的镜面反射。这在现代游戏中也是十分常见的做法(额外添加了预过滤(pre-filtering)来近似微平面BRDF)。但立方体贴图会占用大量的内存空间,因此限制了镜面反射探针(specular probe)的密度,错误的视差(parallax)或遮挡自然会产生一些问题。下图中,由于错误的视差和遮挡,当使用预过滤的环境贴图计算环境镜面反射(environment specular)时,球的边缘反射了自己导致非常亮!
因此需要让光照贴图对镜面反射同样有影响。如果模仿漫反射BRDF,将镜面反射BRDF从积分中提出来,BRDF · Integrate(Lighting · cos($\theta_i$)),而不是原本的Integrate(BRDF · Lighting · cos($\theta_i$)),那么仅仅在观察方向与光照贴图基向量方向接近的时候才能看到些许镜面反射效果。下方示意图展示了改变公式后的效果。
很明显这是错误的,因为兰伯特漫反射BRDF是常量项,可以从积分中提出来,但镜面反射BRDF是与视线方向有关的,不能从积分中提出来。
球谐函数
球谐函数(Spherical Harmonics, SH)是实时图形一种流行的工具,通常作为在离散的探针位置存储间接光照近似值的方式。核心就是在球面上用一系列系数(1个、4个、9个、16个、n*n个)近似出一个关于方向(方向定义在球面上)的分布函数。就像使用一个方向向量从一张立方体贴图上获取特定的值一样。使用低阶的球谐函数只能表示非常低频的信号,下图使用27个系数(RGB每通道9个系数)将HDR图投影到L2球谐函数上。

对于辐射度来讲,低频的球谐函数非常适合。相对于余弦项的入射辐射率积分有效地充当了低通滤波器,非常适合用来与球谐函数去近似辐射度。如果将探针位置或光照贴图的纹素的辐射度投影到球谐函数上,就可以进行球谐查找了(lookup)。通过与系数的点积等一些计算就可以得到球面上任意方向的辐射度。
事实证明,用球谐函数从入射辐照亮度计算辐射度很有用,因为球谐函数表示低频信号是很高效的,在频域中进行简单的乘法就可以完成卷积。在空间域中,与立方体贴图的卷积是$n^{2}$的运算,包含来自辐射率立方体贴图的很多样本。下图为L2球谐函数探针作为漫反射光源照亮的兔子模型。
因此球谐函数是用来近似辐射度的,并且可以在运行时将辐射率转化为辐射度。在探针或光照贴图中存储辐射率的近似值而不是辐射率的近似值(虽然是模糊的版本),这样的低频信号与镜面反射BRDF的乘积进行积分可以得到镜面反射。如果用球谐函数近似辐射度,那么也需要用球谐函数近似BRDF。
然而基于微平面理论的BRDF比兰伯特漫反射BRDF复杂得多。对于漫反射光照,无论材质和观察方向如何,余弦波瓣(cosine lobe)都是相同的。但是镜面波瓣(specular lobe)根据观察方向、材质的粗糙度以及F0的菲尼尔项的不同而变化。本来使用查找表(lookup table,LUT)需要四个参数(观察方向是二维的),但《光环3》中针对球谐函数镜面反射提出了更好的方法。当视线沿着局部Z轴(面法线)旋转时,镜面波瓣的形状不会变化,只有当视线与局部Z轴的夹角发生改变时波瓣形状才会改变(可认为视线绕局部X轴旋转)。因此可以按局部X轴的所有可能的视线方向预计算系数,这样产生的波瓣与实际的观察方向就可以对齐,如图所示: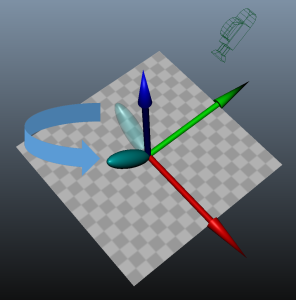
下图展示了计算L2球谐函数光照贴图得到的间接镜面反射项。
使用球谐函数的方法有个常见的问题——“Ringing”现象。当一侧有强光时,在另一侧就会产生负的波瓣,其值就会非常低甚至是负值。对于2D光照贴图不是大问题,因为光照贴图只与面法线的半球入射辐率有关。但对于存储了整个球体的辐射率或辐射度的探针来讲就会有问题。Peter-Pike Sloan提出了一个解决方案,将窗口函数(windowing function)应用于球谐函数的系数,过滤掉Ringing现象,但窗口函数会引入额外的模糊。下图分别展示了蒙特卡洛积分离线渲染结果、投影辐射率到L2球谐函数并计算辐射度产生Ringing现象、应用窗口函数后的效果修正。

