Alex Technical Art

球面高斯函数02——球面高斯函数101

发表于 分类于 Disqus：

本篇是球面高斯函数与预计算光照系列的第二部分，会介绍球面高斯的基础知识——球形径向基函数(spherical radial basis function, SRBF)。本文会介绍一些核心概念，后续的几篇文章会使用这些概念来计算光照贴图或探针中存储的入射光辐射率近似值。

本系列的其他文章可以点击下方链接跳转。

何为球面高斯函数？

球面高斯函数，本质上是定义在球体表面的高斯分布函数。1D的高斯函数就是以e为底的指数函数，下图是以x=0为中心，高度为3的1D高斯函数。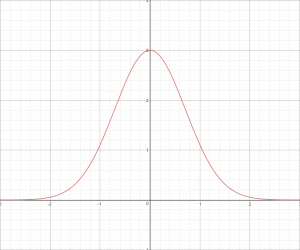

在做图像模糊处理时，也曾听说或使用过高斯模糊，其本质就是使用2D的高斯函数作为滤波器。下图是高斯滤波器应用在2D图像上的白点时的效果。

分布在球面上的高斯函数也是同样的原理，只是维度有了提升，下面是球面高斯示意图。

1D的高斯函数是以下的形式：

(x-b)项使1D高斯函数在笛卡尔坐标系中可以求出给定点到高斯中心的距离。而3D的球面高斯函数参数与1D和2D的不同，需要改变(x-b)项，让高斯函数根据两个单位方向向量夹角进行计算使其作用在球面上。用点积的方式就可以实现：

和普通高斯函数一样，有一些参数可以控制波瓣的形状和位置。参数$\mu$是波瓣的轴向或方向，控制波瓣在球面的位置并且指向波瓣的中心；参数$\lambda$是波瓣的锐度(sharpness)，增加该值时，波瓣会变得更纤细，也就意味着越是远离波瓣轴衰减的越快；参数a是波瓣的振幅或者强度，是波瓣波峰顶部的高度值，可以是标量值，在图形学中也可以是向量，来控制RGB不同颜色通道的变化。在HLSL代码中，只需要球面上一点的标准化方向向量就可以求出该点的球面高斯值。

1
2
3
4
5
6
7
8
9
10
11
12
struct SG
{
  float3 Amplitude;
  float3 Axis;
  float Sharpness;
}

float3 EvaluateSG(in SG sg, in float3 dir)
{
  float cosAngle = dot(dir, sg.Axis);
  return sg.Amplitude * exp(sg.Sharpness * (cosAngle - 1.0f));
}

为何使用球面高斯函数？

球面高斯函数非常直观易于理解，而且很多论文已经探索了球面高斯的使用价值，并对漫反射和镜面反射材质使用球面高斯函数实现了预计算的辐射率传递(pre-computed radiance transfer, PRT)。尤其是《All-Frequency Rendering of Dynamic, Spatially-Varing Reflectance》一文成为RAD工作室使用球面高斯函数的主要参考和灵感。

积运算

对两个高斯函数做积运算可以得到另外一个高斯函数，球面高斯函数也是如此。球面上每个点对两个球面高斯函数进行积运算都会产生另外一个球面高斯函数。实质上就是向量的积运算：

HLSL代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
SG SGProduct(in SG x, in SG y)
{
    float3 um = (x.Sharpness * x.Axis + y.Sharpness * y.Axis) /
                (x.Sharpness + y.Sharpness);
    float umLength = length(um);
    float lm = x.Sharpness + y.Sharpness;
 
    SG res;
    res.Axis = um * (1.0f / umLength);
    res.Sharpness = lm * umLength;
    res.Amplitude = x.Amplitude * y.Amplitude *
                    exp(lm * (umLength - 1.0f));
 
    return res;
}

积分

高斯函数还有一个很好的属性——积分具有一个闭式解，也作误差函数。当然球面高斯也是如此，可以对整个球面做球面高斯积分：

计算积分可以得到球面高斯的总“能量”，对光照的计算很有用。对球面高斯的归一化处理也十分有用(生成一个积分为1的球面高斯)。归一化的球面高斯可以用来表示概率分布，比如法线分布函数(Normal Distribution Function, NDF)。实际上，归一化的球面高斯函数等效于3D中的冯·米塞斯-费舍尔分布(von Mises-Fisher distribution)。

如果移除指数项，计算球面高斯积分开销会很低。随着球面高斯的锐度增加，$(1-e^{-2\lambda})$项的值会很快逼近1，所以只要锐度足够高，就可以在很小的误差范围内将该项移除掉。下图是锐度(X轴)增加时$(1-e^{-2\lambda})$项(Y轴)的数值变化：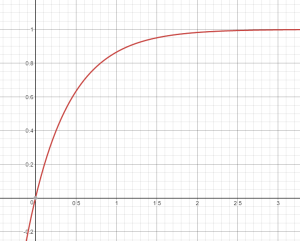

在HLSL实现球面高斯积分的准确版本和近似版本：

1
2
3
4
5
6
7
8
9
10
float3 SGIntegral(in SG sg)
{
    float expTerm = 1.0f - exp(-2.0f * sg.Sharpness);
    return 2 * Pi * (sg.Amplitude / sg.Sharpness) * expTerm;
}
 
float3 ApproximateSGIntegral(in SG sg)
{
    return 2 * Pi * (sg.Amplitude / sg.Sharpness);
}

点积

如果要使用球面高斯积分公式计算两个球面高斯乘积的积分，就是计算两者的点积，通常定义如下：

为了避免数值上的误差可以用下面的形式：

HLSL中的实现如下：

1
2
3
4
5
6
7
8
9
float3 SGInnerProduct(in SG x, in SG y)
{
    float umLength = length(x.Sharpness * x.Axis +
                            y.Sharpness * y.Axis);
    float3 expo = exp(umLength - x.Sharpness - y.Sharpness) *
                  x.Amplitude * y.Amplitude;
    float other = 1.0f - exp(-2.0f * umLength);
    return (2.0f * Pi * expo * other) / umLength;
}

阈值

球面高斯函数支持”紧凑$\epsilon$”，也就是阈值。可以定一个角度，以球面高斯轴的$\theta$弧度内的点的值都大于$\epsilon$。如果将其翻转，就可以计算出锐度$\lambda$，给定弧度$\theta$和$\epsilon$，反求锐度的公式如下：

HLSL实现如下：

1
2
3
4
float SGSharpnessFromThreshold(in float amplitude, in float epsilon, in float cosTheta)
{
    return (log(epsilon) - log(amplitude)) / (cosTheta - 1.0f);
}

旋转

最后一个要讨论的是旋转操作。旋转球面高斯函数很简单：只需要把旋转变换应用到球面高斯的轴向量上。旋转变换可以用矩阵、四元数或者其他方式实现。L1以上的球面高斯需要更复杂的变换。

总要恰饭的嘛